多期二叉树期权定价模型是一种用于对期权进行定价的金融模型。它通过将期权的有效期分解成多个较短的时期，并在每个时期假设期权标的资产价格只有两种可能的变动方向（向上或向下），来近似模拟标的资产价格的随机波动。通过这种方式，模型可以计算出在每个时期末期期权的价值，并最终推导出期权在初始时刻的理论价格。相较于单期二叉树模型，它更能贴近现实市场的波动情况，提高了定价的精确度。这种方法特别适用于那些不满足布莱克-斯科尔斯模型假设（例如，标的资产收益率服从正态分布等）的期权定价。

模型的基本假设

多期二叉树模型建立在以下几个关键假设之上：

离散时间: 模型将期权的有效期限分割成多个离散的时间段（例如，每天、每周或每月）。这与布莱克-斯科尔斯模型的连续时间假设不同。

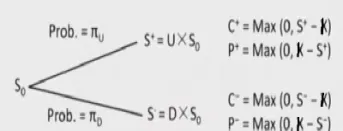
二叉树价格路径: 在每个时间段内，标的资产的价格只有两种可能的变化：向上波动或向下波动。向上波动的幅度通常用 `u` 表示，向下波动的幅度用 `d` 表示，其中 `u > 1` 且 `0 < d < 1`。

无风险利率: 模型假设存在一个无风险利率 `r`，在每个时间段内保持不变。投资无风险资产的回报率是已知的。

无套利机会: 模型假设市场上不存在套利机会。这意味着利用模型的预测，投资者无法通过无风险交易获得超额利润。

恒定的波动率: 在一些简化版本中，模型假设标的资产的波动率在整个期限内保持不变。更复杂的模型允许波动率随时间变化。

模型参数的确定

为了构建多期二叉树模型，我们需要确定以下几个关键参数：

标的资产当前价格 (S): 这是期权标的资产在模型开始时的价格。

执行价格 (K): 期权的执行价格。

到期时间 (T): 期权的到期时间。

时间步长 (Δt): 将到期时间分割成的小时间段， `Δt = T/n`，其中 `n` 是时间段的数量。

无风险利率 (r): 在每个时间段内的无风险利率。

向上波动因子 (u): 标的资产价格在每个时间段内向上波动的倍数。

向下波动因子 (d): 标的资产价格在每个时间段内向下波动的倍数。

波动率 (σ): 标的资产价格的波动率。

`u` 和 `d` 的确定方法有多种，一种常用的方法是基于几何布朗运动模型，利用波动率和时间步长计算：

`u = exp(σ√Δt)`

`d = 1/u = exp(-σ√Δt)`

期权价值的回溯计算

多期二叉树模型采用回溯法来计算期权的价值。从期权到期日开始，计算每个节点的期权价值。

到期日价值: 在到期日，期权的内在价值很容易计算。对于看涨期权，价值为 `max(S<sub>T</sub> - K, 0)`；对于看跌期权，价值为 `max(K - S<sub>T</sub>, 0)`，其中 `S<sub>T</sub>` 是到期日的标的资产价格。

回溯计算: 在每个前一个时间段，期权的价值是其在下一时间段两个可能节点价值的期望值，折算回当前时间段的现值。 具体公式如下：

`C<sub>t</sub> = e<sup>-rΔt</sup>[pC<sub>t+1,u</sub> + (1-p)C<sub>t+1,d</sub>]`

其中：

`C<sub>t</sub>` 是当前时间段的期权价值。

`C<sub>t+1,u</sub>` 和 `C<sub>t+1,d</sub>` 分别是下一时间段向上和向下波动情况下的期权价值。

`p` 是风险中性概率，计算公式为： `p = (e<sup>rΔt</sup> - d) / (u - d)`

`e<sup>-rΔt</sup>` 是贴现因子。

通过重复这个过程，最终可以计算出期权在初始时刻的价值。

模型的优点和缺点

多期二叉树模型相对于单期模型和布莱克-斯科尔斯模型，有其自身优缺点：

优点：

更精确的定价: 通过增加时间段的数量，可以更精确地模拟标的资产价格的波动，提高定价精度。

处理非正态分布: 相较于布莱克-斯科尔斯模型，它可以处理标的资产收益率不服从正态分布的情况。

处理期权的各种特征: 可以应用于各种类型的期权，包括美式期权，因为其离散时间框架允许在每个时间步长评估提前行权的价值。

缺点：

计算复杂度: 随着时间段数量的增加，计算复杂度呈指数增长。

参数敏感性: 模型对参数（特别是波动率）非常敏感，参数的微小变化都可能导致期权价格的较大波动。

对假设的依赖: 模型的有效性取决于其基本假设的准确性。如果实际情况与假设相差较大，模型的定价结果可能存在偏差。

模型的应用及扩展

多期二叉树模型广泛应用于期权定价和风险管理领域，特别是对于那些不满足布莱克-斯科尔斯模型假设的期权。 它还可以扩展到处理更复杂的期权，例如包含期权的期权（例如，期权组合）。一些扩展包括：

允许波动率变化: 在模型中引入时间相关的波动率，以更准确地反映市场的实际波动情况。

考虑股息: 在模型中加入股息因素，以处理支付股息的标的资产。

处理跳跃扩散: 为了更准确反映市场，可以引入跳跃扩散过程来模拟价格突变。

应用于其他金融衍生品: 多期二叉树模型的思想可以扩展到其他金融衍生品的定价，例如利率衍生品。

多期二叉树模型提供了一种相对简单但有效的期权定价方法，虽然其计算复杂度会随着时间段数的增加而增加，但通过现代计算技术，这已不再是主要的限制。通过合理的参数选择和模型扩展，多期二叉树模型可以为金融从业者提供有价值的期权定价和风险管理工具。